A Short Course on Sound and Human Hearing - Part 2
Jed Margolin
Index
4. The Fundamentals of Harmonics
There are two types of sound waveforms: periodic and non-periodic.
Periodic waveforms repeat themselves over and over. Theoretically, they have no beginning and no end. In reality, they only have to go on for “long enough” where “long enough” depends on what you are using it for.
This example of a periodic waveform is two periods of a sine wave. The amplitude goes between +1 and -1. The period is 1.0 ms.
Figure 1
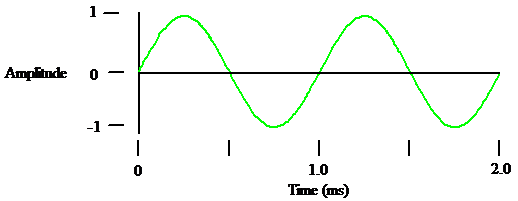
Frequency = 1/Period, so the frequency = 1/1ms = 1,000 Hz.
Other examples are:
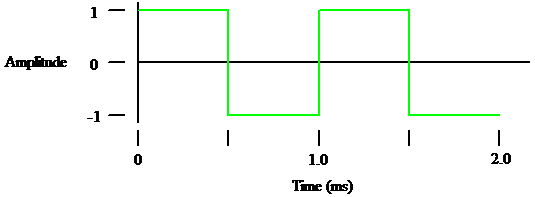
Square Wave
Figure 2
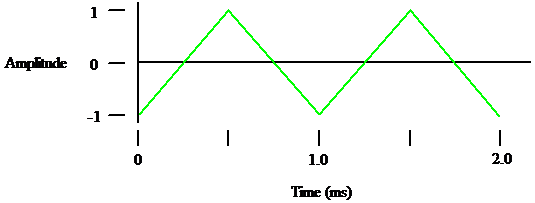
Triangle Wave
Figure 3
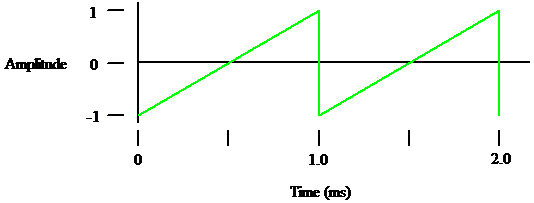
Sawtooth
Figure 4
Periodic waveforms do not have to go between +1 and -1.
Figure 5
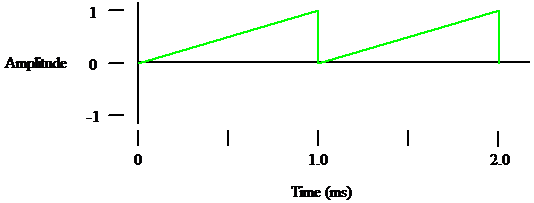
And they don’t have to be pretty. They just have to repeat themselves.
Figure 6
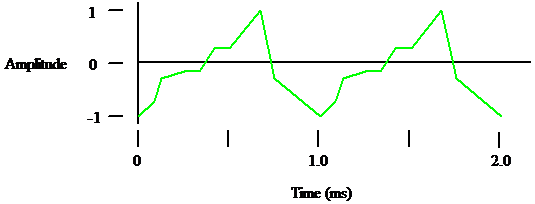
But they do have to be able to exist in the real world.
Figure 7
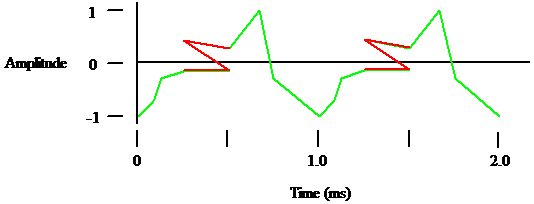
They cannot have more than one value at the same time. (We will leave the possibility of quantum superposition of sound waveforms to the theoretical physicists.)
Not all sound waves are periodic.
There are impulses that happen only once.
Figure 8
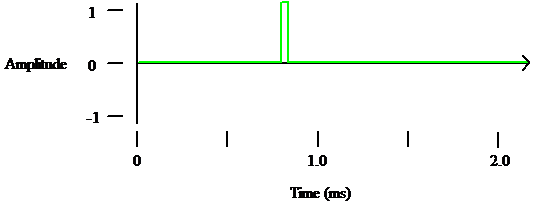
(Thump)
And there is random noise.
Figure 9
2. What is Sound?
So far we have referred to Amplitude without saying Amplitude of What.
The Amplitude could be the voltage level of an electrical signal that will be sent to a speaker which will turn it into a sound pressure, which is actually a change in sound pressure.
Or, the Amplitude could be the change in sound pressure itself.
Sound is a pressure wave that travels through a medium, which can be a gas, a liquid, or a solid. In this article we are interested only in sound that travels through a gas (the air).
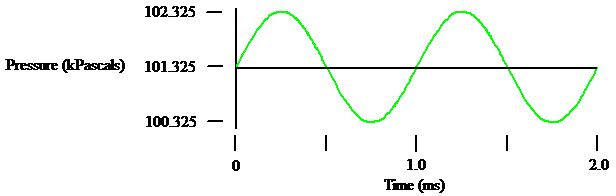
The sound wave is a change in the pressure as it travels through the atmosphere. The Amplitude is how much the sound wave changes the atmospheric pressure.
At Sea Level the standard atmospheric pressure is 760 mm mercury = 760 Torr = 101,325 Pascals =
101.325 kPascals = 101.325 millibars = 1.0132 x 105
A sound wave compacts (increases) and rarefies (decreases) the air pressure as shown in this example.
Figure
10
One of the consequences of this is that there is a maximum undistorted sound level that can exist in the atmosphere that depends on the barometric pressure.
Figure
11
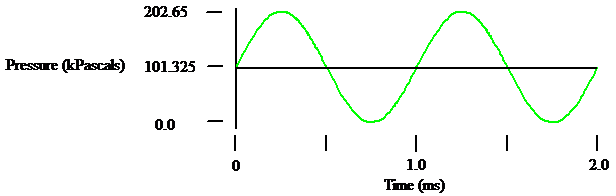
The sound pressure can be higher than 202.65 kPascals but it cannot be less than 0 kPascals. 0 kPascals is a vacuum. The sound wave would clip.
Figure
12
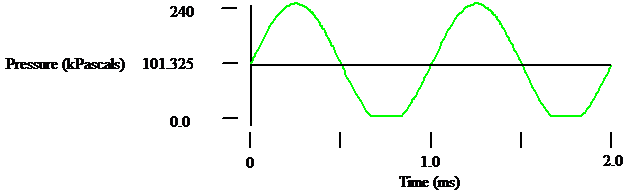
For a sine wave at a barometric pressure of 101.325 kPascals the clipping point is 191.1 dBA.
Sound is a longitudinal wave, which means that compactions and rarefactions occur along the direction that the wave is travelling.
And, not surprisingly, sound travels at the speed of sound.
But the speed of sound depends on several things, like temperature, humidity, and air density.
From: http://www.aerospaceweb.org/design/scripts/atmosphere/
And http://www.altitude.org/air_pressure.php
|
|
Sea Level |
4,500 feet |
6,000 feet |
|
Atmospheric Pressure |
1013 mb |
859 mb |
812 mb |
|
Air Density (Ratio) |
1.00 |
0.875 |
0.836 |
|
Speed of Sound |
761.2 mph 1,116.45 ft/sec |
749.4 mph 1,099.05 ft/sec |
745.4 mph 1,093.20 ft/sec |
|
Oxygen |
100% |
86% |
81% |
(The percentage of oxygen is not a factor in how sound travels. I included it because it is interesting.)
If you stand in a fixed location the compactions and rarefactions whiz by you.
If you are traveling with the wave you will be covering some distance. What distance is that?
Waves have a fundamental relationship between speed, frequency, and wavelength (the length of one period of the wave):
velocity = frequency * wavelength.
This can be rearranged as:
wavelength = velocity / frequency
For example, at sea level where the speed of sound (velocity) is 1,116.45 ft/sec, a 1 KHz sound wave has a wavelength of 1.12 feet. At an altitude of 4,500 feet the wavelength is 1.10 feet. At 6,000 feet it is 1.09 feet. The difference doesn’t sound like much.
But for 20 Hz the wavelength is 55.82 feet (Sea Level), 54.95 feet (4,500 feet), and 54.66 feet (6,000 feet).
The difference between Sea Level and 6,000 feet is 1.16 feet. It still doesn’t sound like much but it may be enough to make a difference in speaker design as well the design of sound barriers for low frequencies.
The decrease in air density definitely has an effect on the free-air-resonance of several subwoofer speakers I have tested.
Here is a chart of altitudes, frequencies, and wavelengths.
|
Speed of Sound (ft/sec) |
Frequency (Hz) |
Wavelength (ft) |
|
|
|
|
|
Sea
Level |
|
|
|
1116.45 |
1000 |
1.12 |
|
1116.45 |
440 |
2.54 |
|
1116.45 |
20 |
55.82 |
|
1116.45 |
12 |
93.04 |
|
|
|
|
|
4,500
ft |
|
|
|
1099.05 |
1000 |
1.10 |
|
1099.05 |
440 |
2.50 |
|
1099.05 |
20 |
54.95 |
|
1099.05 |
12 |
91.59 |
|
|
|
|
|
6,000
ft |
|
|
|
1093.2 |
1000 |
1.09 |
|
1093.2 |
440 |
2.48 |
|
1093.2 |
20 |
54.66 |
|
1093.2 |
12 |
91.10 |
At Sea Level, a room with one of the dimensions being 55.82 feet will have a resonant node at 20.0 Hz.
That same room at 6,000 will have the resonant node at 19.58 Hz.
At 12 Hz, a room with one of the dimensions being 93.04 feet will have a resonant node at 12.0 Hz. That same room at 6,000 feet will have the resonant node at 11.75 Hz.
Whether or not that makes a difference (such as for a school gymnasium) depends on how finely tuned a County’s Sound Ordinance is.
4. The Fundamentals of Harmonics
Jean Baptiste Joseph Fourier (1768 - 1830) was a French mathematician and physicist. One of the things he did during his life was to develop (discover?) the powerful tool that bears his name: Fourier Analysis.
In Fourier Analysis, any periodic waveform can be represented as an infinite series of sines and cosines. They are not just any sines and cosines, they are multiples of the frequency corresponding to the period of the periodic waveform.
For example, if the period of the waveform is 0.1 second the frequency is 10 Hz (1/0.1) and the series of sines and cosines will be at 10 Hz, 20 Hz, 30 Hz, 40 Hz, etc. The frequency corresponding to the period of the waveform is called the Fundamental Frequency. Technically, it is also called the First Harmonic. 20 Hz is the Second Harmonic. 30 Hz is the Third Harmonic, and so on.
The math can be daunting unless you are a Mathematician, Physicist, or Engineer. (Fourier Analysis is at least a college semester course.) I will keep the math to a minimum. Then I will give a simpler explanation.
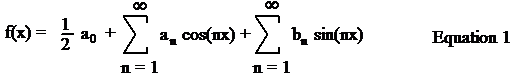
Where:
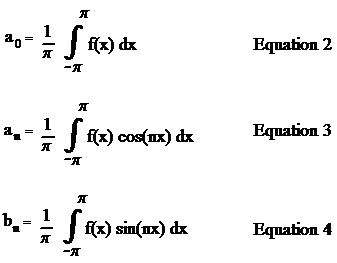
Math Notes
1. In Equation 1 the symbol
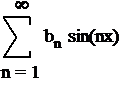
means we are to sum the terms
bn * sin (n*x)
for n = 1 to n = infinity.
The first few terms are:
b1 * sin(1*x) + b2
* sin(2*x) + b3 * sin(3*x) + b4 * sin(4*x) + ………
(1*x) is the Fundamental Frequency, (2 *x) is the Second Harmonic, (3*x) is the Third Harmonic, etc.
The coefficients b1, b2,
b3, etc. are the amplitudes at those frequencies.
The idea of infinity can be unsettling, but most waveforms need much less than that to be “close enough.”
2. The function f(x) that results from Equation 1 (and is used in Equations 2 - 4) is the arbitrary (but periodic) waveform that we want to represent as an infinite series of sines and cosines.
A good introduction to Fourier Analysis can be found at http://www.facstaff.bucknell.edu/mastascu/elessonshtml/Freq/Freq4.html
An explanation that goes more deeply into the math can be found at Wolfram Math World.
http://mathworld.wolfram.com/FourierSeries.html
Simpler Explanation
The following is a simpler explanation of the Fourier Series.
Think of it as a tunable filter. Imagine you are tuning an AM radio across the band. When you come to a station you note its frequency (position on the dial) and its signal strength.
Now, instead of an AM radio with stations that can be located anywhere on the dial, start with one frequency. In this example our periodic waveform has a frequency of 100 KHz. Tune the filter to 200 KHz (Second Harmonic) and note the signal strength. Now tune to 300 KHz and note the signal strength. Then 400 KHz, etc.
A waveform with a period corresponding to a frequency of 100 KHz can only have harmonics that are a multiple of 100 KHz.
That doesn’t mean that every waveform has energy at all of the harmonics.
For example, a square wave has only odd harmonics (n= 1, 3, 5, 7, etc.)
In addition, a square wave does not have to have a 50% duty cycle like this one has.
Figure 13

The following square wave has a 25% duty cycle.
Figure 14
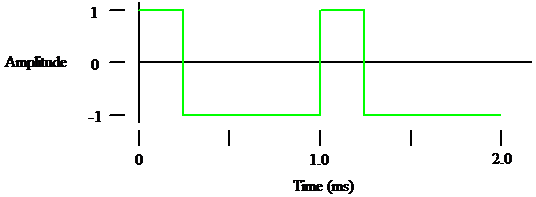
As the duty cycle is reduced more of the energy goes into the higher harmonics.
The triangle wave (Figure 3) also contains only odd harmonics but the amplitudes of the harmonics fall off more quickly than for the square wave.
The sawtooth (Figure 4) contains both even and odd harmonics.
Paul Falstad has written an excellent java applet demonstrating the Fourier Series for different waveforms.
http://www.falstad.com/fourier/
You can run the applet for each waveform separately.
http://www.falstad.com/fourier/e-index.html
Or you can run an applet that allows you to choose the waveform from an applet.
http://www.falstad.com/fourier/index.html
Don’t forget to check the box labeled “sound”. If your computer has sound capability you will hear the waveform. Hopefully, you have either decent speakers or decent headphones.
5. Why all of this matters
A County has an Ordinance regulating wind turbines which includes the sound frequencies and sound levels that wind turbines may produce at a specified distance from the wind turbine. The reason for these limits is to protect residents not only from harmful effects of the sound but to preserve the peace and quiet that the residents have the right to enjoy.
The Ordinance must also accommodate the right of wind turbine operators to install and operate wind turbines.
The Ordinance must be reasonable to both parties or, if the County were sued (by either party), the County would lose.
A demonstration is proposed to play sounds at the frequencies and levels allowed by the Ordinance to determine whether they are reasonable.
a. The Ordinance makes the statement that the range of human hearing is 20 Hz to 20 KHz. Because of that, the sound levels permitted below 20 Hz are substantially higher than for frequencies above 20 Hz.
A demonstration to play sounds below 20 Hz is proposed, using pure tones (sine waves).
The County challenges the use of pure tones but offers no waveform of its own.
Answer:
If a periodic waveform of a sine wave is not used, there will be harmonics.
For example, take a periodic waveform played at 18 Hz. The harmonics of 18 Hz are 36 Hz, 54 Hz, 72 Hz, 90 Hz, 108 Hz, 126 Hz, etc.
Some of these harmonics may not be present, such as if a square wave is used. A square wave has only odd harmonics, so there will be energy at 54 Hz, 90 Hz, 126 Hz, etc.
These higher harmonics will be in a range that is clearly audible, and since the test was to determine whether people can hear 18 Hz, the test will be invalid.
Take the example of a waveform played at 12 Hz. The harmonics of 12 Hz are 24 Hz, 36 Hz, 48 Hz, 60 Hz, 72 Hz, 84 Hz, etc.
Again, some of these harmonics may not be present, such as if a square wave is used. A square wave has only odd harmonics, so there will be energy at 36 Hz, 60 Hz, 84 Hz, etc.
These higher harmonics will be in a range that is clearly audible, and since the test was to determine whether people can hear 12 Hz, the test will be invalid.
b. The Ordinance allows sound levels at frequencies below 60 Hz to be substantially higher than for frequencies above 60 Hz. This is due to the statement that human hearing is 20 Hz to 20 KHz and by using the Sound Pressure Meter A-Weighting, which is based on the Fletcher Munson curves.
In order to determine whether these frequencies and limits are reasonable, a demonstration to play sounds at the frequencies and level permitted by the Ordinance below 60 Hz is proposed, again by using pure tones (sine waves).
Again, the
Answer:
The same arguments apply here as in the example in the above paragraph. Any periodic sound not using sine waves will contain harmonics that will make the test invalid.
In addition, the Ordinance bases its allowable limits on sources that trace their lineage back to Fletcher-Munson, who used pure tones (sine waves) to derive their curves.
c. The Ordinance calls for the use of a Type 1 meter using 1/3 octave filters to measure sound levels. This filters out the higher harmonics of any periodic waveform. Effectively, it measures only the fundamental frequency, which is a pure tone (sine wave). It’s ok for the meter to measure only a pure tone but it’s not ok for people to listen to one?
d. Since any periodic waveform that is not a sine wave will contain harmonics, the equipment used to perform a demonstration must be able to produce a sine wave at the frequencies without distortion. If either the amplifier or the speaker distorts the sine wave, then harmonics will be produced. Speaker systems are more likely to produce distortion because they are limited by the physics of sound reproduction.
e. The issue of whether or not sounds having a frequency and level allowed by an Ordinance are reasonable is not a matter to be decided by Acoustics Experts.
Suppose a County enacts an Ordinance allowing residents to be subjected to sounds at certain frequencies and levels, and the County leaders refuse to sit through a demonstration of those sounds. The residents may be subjected to these sounds 24 hours a day, seven days a week. The County leaders would only have to endure the sounds for a 20 minute demonstration.
If they refuse, then the Ordinance is open to a legal challenge and the presumption is that the sound frequencies and levels allowed by the Ordinance are unreasonably high.
Jed Margolin
September 6, 2010